位运算符
位运算符
关于位运算符无非也就 与(&)、或(|)、异或(^)、取反(~)、左移(<<)、右移(>>)、无符号右移(>>>)
位运算其实就是二进制的运算,加减乘除适用于十进制,而位运算就是二进制的运算,但是由于我们的运算都是基于十进制来说的,所以会有点绕,略微有点难懂,接下来言归正传
与运算符(&)
4&7
我们需要把两个二进制转换成十进制
4:0000 0100
7:0000 0111

这里提到一点:1表示true,0表示false
而与运算的时候相同位之间其实就是两个Boolean的运算
全true(1),即为true(1)
全false(0),即为false(0)
一false(0)一true(1),还是false(0)
或运算符(|)
以 5|9 为例
5 : 0000 0101
9 : 0000 1001

在做与运算的时候
遇true(1)就是true(1),
无true(1)就是false(0)
异或运算符(^)
以 7^15 为例
7: 0000 0111
15: 0000 1111

在异或的时候
只要相同都是false(0)
只有不同才是true(1)
一个数连续异或同一个数两次,结果是它本身
取反运算符(~)
例: ~15
同样的先变成二进制:15:0000 1111

这个其实挺简单的,就是把1变0,0变1
注意:二进制中,最高位是符号位 1表示负数,0表示正数
左移运算(<<)
左移就是把所有位向左移动几位
如: 12 << 2 意思就是12向左移动两位
12的二进制是: 0000 1100
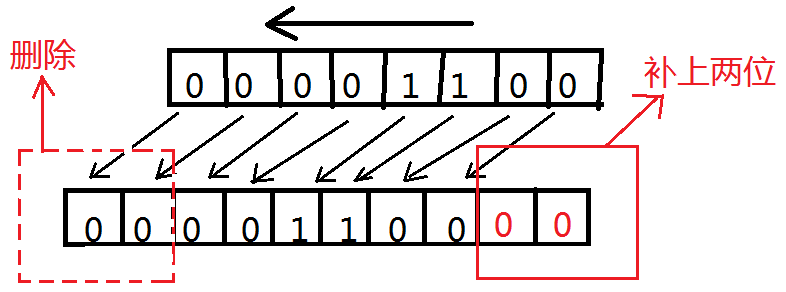
通过这个图我们可以看出来,所有的位全都向左移动两位,然后把右边空的两个位用0补上,最左边多出的两个位去掉,最后得到的结果就是00110000 结果就是48
我们用同样的办法算 12<<3 结果是 96
8<<4 结果是 128
由此我们得出一个快速的算法 M << n 其实可以这么算 M << n = M * 2n
右移运算符(>>)
这个跟左移运算大体是一样的
例: 12 >> 2
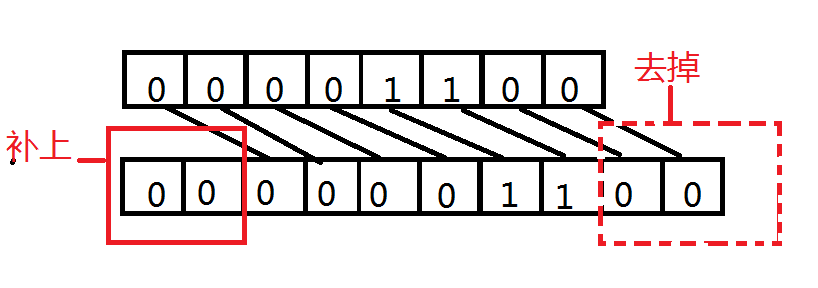
我们可以看出来右移和左移其实是一样的,但是还是有点不同的,不同点在于对于正数和负数补位的时候补的不一样,负数补1,正数补0
如我们再做一个 –8 的 -8>>2
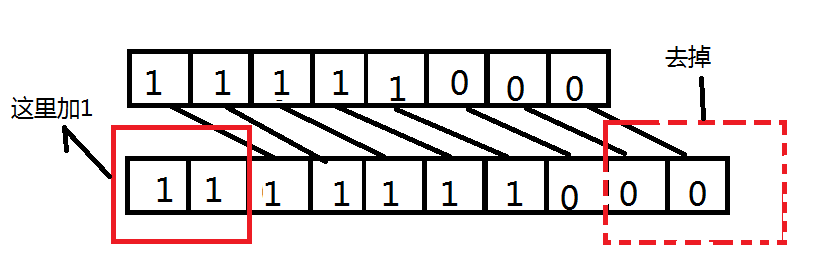
这里总结一下,关于负数或者正数来说,移位的时候是一样的,但是在补位的时候,如果最高位是0就补0,如果最高位是1就补1
由此我们得出一个快速的算法 M >> n 其实可以这么算 M >> n = M / 2^n
无符号右移(>>>)
无符号右移(>>>)只对32位和64位有意义
在移动位的时候与右移运算符的移动方式一样的,区别只在于补位的时候不管是0还是1,都补0




